développement puissance cadence pente

Petites mathématiques appliquées au cyclotourisme tranquille, pour des choix de développements raisonnés.

La pente (1), la cadence (2), 

la puissance (3) et le développement en montagne (4).

Quand je suis arrivé à l'Union Cycliste Nantaise (UCN, devenue UCNA , avec un A d'Atlantique depuis), je faisais du cyclotourisme depuis une trentaine d'années. Sans le savoir, sans y avoir réfléchi. Ce qui ne m'empêchait pas de pédaler. En fréquentant des touristes à vélo plus expérimentés et plus savants que moi, à l'UCN-A et ailleurs, j'ai entendu parler de braquet, de développement, de cadence, de vélocité, etc. Les opinions sur ces sujets sont diverses. Les débats sont permanents. L'échange d'idées, c'est la vie. Un aperçu de la section cyclotourisme de l'UCNA est visible là UCNA section cyclotourisme.

J'ai un peu mieux compris les notions propres au vélo, en lisant un peu, en échangeant avec les uns et les autres, et en calculant. Les chiffres m'ont permis surtout de pouvoir répondre par avance à quelques questions que je me suis posées avant de me lancer dans l'inconnu d'alors, comme la montagne ou le cyclo-camping.

N'étant pas matheux, ni pour un rond, ni pour un triangle, je tâtonne comme je peux avec mes moyens limités. Les connaisseurs jugeront peut-être que je redécouvre l'eau tiède. Mais qu'importe. Je livre mes petits calculs avec une modestie sincère. Mon but étant de mieux appréhender ma pratique de la bicyclette, j'accueillerai avec reconnaissance les rectifications et précisions des spécialistes.

1 Le pourcentage de la pente.

Tout en pédalant, je me suis posé à l'occasion la question de la meilleure manière d'exprimer la pente. Des panneaux au bord des routes nous informent sur des pourcentages, quand ils sont supérieurs à une certaine intensité, disons 5% sur les routes « normales. » Je prends un exemple pour tenter de m'y retrouver. Étant limité en savoir chiffré, je me contente de considérer que toute route en pente peut, de profil, se réduire à un triangle rectangle. Avec les triangles moins bourgeois, j'ai plus de difficultés. Pour les profils irréguliers, il est possible de découper en une série de triangles rectangles. Soit donc un triangle rectangle bon père de famille qui aurait cette mine là

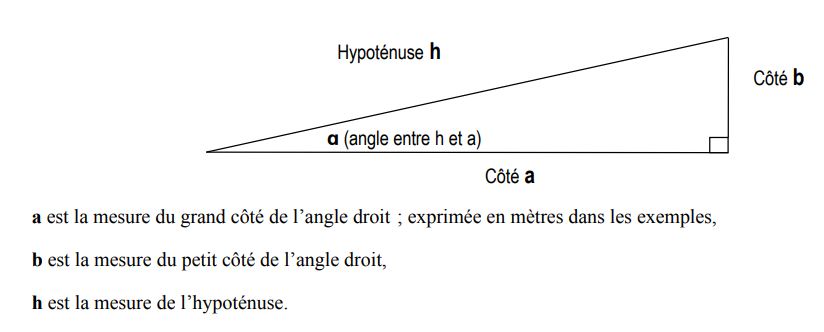
Le dénivelé s'obtient en soustrayant l'altitude du bas de la pente à celle du haut. Je calcule le pourcentage d'une pente en divisant le nombre de mètres de dénivelé (ici la longueur de b) par la distance parcourue, l'hypoténuse h. Pour un dénivelé de 100 mètres et une distance parcourue de 1000 mètres, je calcule donc : 100 / 1000 = 0,1. Le dénivelé pour un mètre est de 0,10 m. Je multiple par 100 pour obtenir un dénivelé pour cent mètres, soit 10 mètres pour 100 mètres, ce qui s'écrit 10 %. Du coup, j'ai l'impression de comprendre les panneaux, et les chevrons des cartes Michelin. Madame IGN met à disposition des enseignants et des grandes personnes désireuses d'apprendre une page utile à la lecture des cartes.

J'ai lu quelque part (ça, c'est de la rigueur dans la citation !) certains professent que le pourcentage se calcule non pas par rapport à la distance parcourue, l'hypoténuse h, mais par rapport à la distance linéaire, soit le grand côté a. Comment faire pour obtenir ce a ? Grâce à ce vieux Pythagore, qui dit que h² = a² + b². Une petite calculette toute simplette permet d'obtenir rapidement que a = 994,98 mètres. Ma pente est donc de (100 / 994,98 ) x 100 = 10,05 %.

La différence avec mes 10 % de ci-dessus ne vaut pas la peine de se fatiguer la tête, et très probablement rend inutile un changement de braquet ! Cette différence s'accentue un chouia avec le dénivelé pour une même distance parcourue. Quand b est de 150 m et que a reste à 1000 m, j'obtiens 15 % par rapport à h, mais 15,17 % par rapport à a. En gros, le rapport dénivelé/distance parcourue est à peu près semblable au rapport dénivelé/distance linéaire. L'approximation continuera de suffire à mon bonheur de pédaleur tranquille. Pour les constructeurs de chemins de fer ou de routes, ou les couvreurs, etc. cette approximation pourrait s'avérer trop vague.

Le degré de la pente.

Plus rarement, une pente peut aussi s'exprimer en degrés. Si vous estimez n'avoir que faire des degrés dans les pentes, sautez ce paragraphe et allez à la cadence (un texte peut être une sorte de jeu de l'oie, on est pas obligé d'ânnonner ligne par ligne).

Il me fallait donc trouver comment calculer l'angle α dont les côtés sont h et a. Je suis allé voir sur Internet. De nos jours, des explications qui m'ont semblé assez claires sont gracieusement fournies par des matheux plus désireux de répandre leur savoir que de sélectionner de futurs initiés. Donc rien à voir avec les dragons qui m'ont stupidement gâché les mathématiques pendant mon adolescence. En appliquant mécaniquement une formule de base de la trigonométrie, ça donne pour b = 100 mètres de dénivelé et h = 1000 mètres de distance parcourue : sin(α) = b / h = 100 / 1000 = 0,1. Mon autre calculette, à peine plus scientifique que la simplette, m'apprend que l'angle correspondant (d'après sin(α)-1 également tapoté sur ma calculette) est de 5,74°.

Ainsi, une pente à 10 % fait moins de 6 degrés ! Et une pente à 5 % ne fait que 2,9 degrés. Une pente à 5 %, c'est une élévation de 50 mètres en 1 km. Un type de bosse bien commun en nos contrées... Ça relativise... Ou, plus exactement, ça démontre que l'expression de la pente en degrés ne m'est pas suffisamment familière pour paraître adaptée. Elle semble sous-estimer une réalité que nous connaissons mieux sans doute avec nos jambes qu'avec notre tête, et cette expression en chiffres moins gros ne me donne même pas l'impression de moins forcer... 

Je répète n'être pas matheux. J'ai toujours des doutes à propos du résultat de mes calculs. Ce dont je suis certain par contre, c'est que l'indication des pourcentages a tendance à disparaître des cartes. Les chevrons se font plus rares ou plus approximatifs lorsque les routes sont moins fréquentées par les automobiles. Ce sont précisément ces routes tranquilles que nous recherchons. M. Michelin, je ne vous dis pas merci. Qu'il les apprécie ou les évite, le cyclotouriste a besoin de l'indication des pourcentages.

2 La cadence.

Certains cyclistes tournent très vite les pieds pour avancer. D'autres, pour avancer à la même vitesse, tournent plus lentement. Les grands, pas tous sans doute, ont tendance à utiliser une plus faible vitesse de rotation du pédalier que les petits. Un tour de pédalier correspond à une rotation complète d'une pédale, la cadence étant le nombre de tours par minute, ou rotation par minute, dite RPM. Cette cadence dépend aussi, pour chaque individu du type de fibres musculaires qui dominent, de la souplesse articulaire, des capacités athlétiques innées et, pour une part, acquises par l'entraînement.

Dans ce domaine comme dans à peu près tous les autres, il n'existe pas de règle valable partout pour tout le monde. L'observation, et une très sérieuse thèse de doctorat, ont démontré cependant que les coureurs tournent aux alentours de 90 à 100 tours de pédalier à la minute, les cyclotouristes vers 80 et le promeneur occasionnel est plutôt à 60 tours-minute. Les cyclotouristes traditionnels considèrent qu'il faut tourner entre 75 et 90, c'est à dire qu'ils mettent plus grand quand ils atteignent 90 tours-minute, et un développement plus petit quand ils passent sous les 75 tours-minute.

Il y a des exceptions dans tous les sens. Ainsi, exemple cité par Jean Bobet, Arthur-Augustus Zimmerman dit le « yankee volant », brillant sprinter des années 1888 à 1896, disposait d'une fabuleuse vélocité malgré ses 1,82 m et une posture sur le vélo qui nous semble aujourd'hui curieuse. Sur 100 m lancés, il tournait à 184 tours-minute, soit 3 tours de pédalier à la seconde, soit 6 coups de pédale à la seconde ! Et nous connaissons tous des petits gabarits qui emmènent sans coup férir leur roue à aube avec majesté sur de longues distances.

Chacun peut trouver sa vitesse de jambes par essais successifs. À l'issue de plusieurs sorties où le cycliste aura tourné les jambes un peu moins vite, puis de plusieurs sorties où il aura tourné un peu plus vite, et surtout de son état comparé à l'arrivée, il pourra faire le choix qui lui convient, plus en force ou plus en vélocité. La cadence, ou nombre de tours-minute, se calcule ainsi :

vitesse en mètres par heure / (nombre de dents du plateau avant / nombre de dents du pignon arrière) x circonférence de la roue x nombre de minutes en une heure = nombre de tours-minute

Par exemple à 23,7 km/h sur 40/17 en 700c : 23 700 / (40 / 17) x 2,1 x 60 = 80 tours-minute.

On peut, pour faire les essais, se composer un petit tableau du genre de celui qui suit (avec une roue de 700 C, soit 2,1 m de circonférence), où la vitesse s'obtient en multipliant le développement par la cadence, puis en re multipliant par 60, parce que les heures font 60 minutes, et en divisant le tout par 1000 pour passer des mètres aux km. Ainsi, pour un développement de 5,25 m (40 / 16 x 2,1) et une cadence de 80 tours-minute :

5,25 x 80 x 60 = 25200 mètres à l'heure, soit 25,2 km/h.

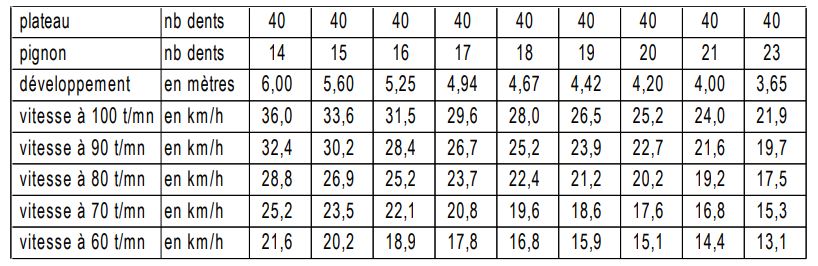Ce type de tableau, que chacun pourra se composer en fonction de ses plateaux et roue-libre, peut aussi servir à des constats sur la cadence utilisée couramment. Un compteur affichant en direct la cadence de pédalage évite les calculs, mais est encore plus utile si on sait pourquoi et comment on s'en sert. La cadence est en partie un acte volontaire que l'on peut modifier par l'entraînement, dans certaines limites propres à chaque individu.

3 La puissance.

Souvent confondue avec la seule force, la puissance résulte de la combinaison de la vitesse avec la force. Un cycliste produit la même puissance en tournant vite un petit développement qu'en tournant lentement un développement plus grand. Elle se calcule en Watt, avec la formule suivante :
P = Kg x G x V x %
P : puissance en Watt
Kg : poids du cycliste + vélo + bidons + sacoche(s), ici 85 kg
G : gravité (9,81, considéré ici comme constante à toute altitude)
V : vitesse en mètres par seconde (= vitesse en mètres/h / 3 600) ; ici 9 km/h => 9000 m/h => 2,5 m/s,
% : pourcentage de la pente (voir partie 1.1), ici 10 %, écrit 0,1
Exemple : 85 x 9,81 x 2,5 x 0,1 = 208 Watt
Avec cette petite formule, il n'est pas nécessaire de disposer d'une machinerie sophistiquée pour calculer la puissance. Une calculette simplette et un vélo habituel pourvu d'un banal compteur suffisent. Ce calcul peut être utile, par exemple, pour relativiser l'importance du poids du vélo (voir ci-dessous.) Il peut aussi permettre de savoir si on peut monter une pente supérieure avec plus de poids (disons 120 kg bagages compris), pour préparer un voyage en cyclo-camping. Mettons que le cyclo-campeur espère qu'on peut rouler à 5 km/h dans un 12 % avec 208 Watt maximum, puis calculons : 120 x 9,81 x 1,39 x 0,12 = 196 Watt => il peut le faire !

Certains ont plus de puissance que d'autres. Il semblerait...

4 Les développements en montagne

Comment les choisir ? Carlo Bourlet, mathématicien et membre de l'Académie des sciences, en 1899, a rédigé un ouvrage qui reste une référence : La bicyclette, sa construction, sa forme. Carlo écrit notamment : « Tout cycliste sérieux devrait calculer le développement qu'il doit adopter. Il lui suffit pour cela d'avoir déterminé une première fois par des essais et tâtonnements consciencieux quel est le développement maximum avec lequel il peut gravir sans efforts extraordinaires, sans battements de cœur et sans essoufflement, une côte de pente connue à une petite allure de 8 à 9 km à l'heure. » Connaissant la pente (5 %) et le développement (5 mètres) que notre cyclotouriste léger utilise pour gravir confortablement la susdite pente, notre vaillant cycliste peut user de la formule de Carlo :

X = ((0,01 + P) / (0,01 + Q)) x D
X est le développement recherché,
P est la pente connue ; ici 5 %, qu'on écrit 0,05 (= 5 / 100),
Q est la pente que l'on envisage de franchir, ici 10 %, sous la forme 0,1
D est le développement utilisé pour franchir en fumant la pipe la pente à 5 %, 5 mètres dans ce cas.
À nos calculettes : X = ( (0,01 + 0,05) / (0,01 + 0,1) x 5 = (0,06 / 0,11) x 5 = 2,72 mètres, soit à peu près un 30/23 en 700 C.

En triturant un peu la formule de la puissance, toujours pour 208 Watt et 85 kg, notre cycliste décidément sans reproche gravira cette future pente à 10 % à la vitesse suivante : 85 x 9,81 x 0,1 x V = 208 => V = 208 / 83,385 => V = 2,49 m/s, soit 9 km/h.

Ce dernier calcul n'est qu'une adaptation de la formule du point 3. En appliquant cette même formule malaxée, et si on considère qu'il diminue le poids de 2 kg grâce à un vélo plus léger, il pourra porter sa vitesse à 9,2 km/h. Bof ! Le cyclo-campeur avec ses 120 kg et 208 Watt TVA comprise, fera du 6,36 km/h dans la même pente à 10 %. Et s'il gagne 5 kg (c'est énorme !), du 6,6 km/h, soit un gain de 0,24 km/h... Encore plus bof ! Un gros malin vous dirait que ça fait un gain de 4 %. C'est un gros malin. 4% sont importants pour un coureur, toute différence est bonne à prendre pour lui. Un cyclotouriste vit bien sans rien en savoir. Un voyageur s'en moque éperdument.

En continuant les calculs, si le cycliste léger (85 kg avec le vélo, la sacoche de guidon, les bidons et le bonhomme habillé) monte ses 10 % à 6,5 km/h, c'est qu'il dispose de 150 Watt. Le cyclo-campeur, avec 150 Watt, gravira la côte à 10 % à 4,5 km/h. Il lui faudra, à 50 tours-minute, un développement de l'ordre de 1,5 m, soit avec à peu près un plateau de 20 dents (Si ! Si ! Ça existe !) et un pignon de 28. Il est pas rendu, comme on dit chez nous. Il s'en fout. Il est pas pressé.

Ces exemples de calculs tiennent pour négligeables les forces de frottement. Elles ne le sont pas tout à fait, même si elles ne sont pas majeures. A cette allure, contrairement à ce qu'un vain peuple pense, un pneu de 30 mm de large correctement gonflé sera plus efficace que son compère de 22 mm. Il est aussi plus confortable et moins fragile. À chacun selon son choix. Cha ch'est ben vrai !

transmission de cyclo campeur pour grimper aux arbres : plateaux de 40, 34 et 20 avec pignons de 14 à 28

Commentaires finaux (ou finals).

Un des avantages des calculs, c'est que les chiffres ont une apparence de neutralité. Disposer de 100, 200, 300 ou 400 Watt n'est ni honorifique ni déshonorant, pas plus ni moins que de tourner à une cadence de pédalage de 50 ou 120 tours-minute. C'est une donnée, un peu comme le temps qu'il fait. Ça dépend des capacités athlétiques de base héritées des ancêtres et de la quantité de cheveux blancs du moussaillon. On peut faire mieux, ou se maintenir au mieux, en s'entraînant. Chez le débutant, la progression résultant de l'entraînement régulier peut être spectaculaire, d'autant plus si elle s'accompagne d'une hygiène de vie améliorée ; elle est bénéfique pour la santé et satisfaisante sur le plan psychologique. Mais on ne pourra passer de 150 à 450 Watts, même avec de la poudre de perlimpinpin dans le bidon et un vélo tout titane. Le cyclotouriste se fait plaisir avec ce qu'il a.

L'expérience apprend que rien ne vaut... l'expérience, pour autant qu'on y ajoute une poignée d'observation, une bonne louche d'échanges avec les autres touristes à bicyclette, et une petite pincée de réflexion de temps en temps. Les calculs contribuent à cette réflexion, même s'ils n'en sont qu'une partie et qu'une manière de l'aborder, parmi d'autres. Je connais des personnes qui ne se fient pas aux calculs, ou n'en éprouvent pas le besoin, mais qui ont assez de jugeote pour faire les choix qui leurs conviennent. Le bon sens est-il bien partagé ? Les calculs ne permettent pas de répondre à cette question. Du moins, pas à ma connaissance, mais, et je crois l'avoir dit, je ne suis pas spécialiste.

Les compteurs sont pratiques, si on sait les lire

Les compteurs sont de plus en plus sophistiqués. Ce qui réclamait auparavant des calculs plus ou moins savants peut être donné en direct par les ordinateurs de plein air spécifiques aux bicyclettes : vitesse, distance évidemment, mais aussi cadence, développement, puissance, altitude, pente, cumuls et moyennes de tout ça et de bien d'autres choses. Génial. À condition de maîtriser les notions, d'avoir la patience de lire les mode d'emploi pour se familiariser avec la bête, et le porte-monnaie suffisamment garni. Les prix baissent un peu alors que le nombre de fonctions augmente, mais ils demeurent relativement élevés, de l'ordre de 150 à 400 € pour disposer de toutes les fonctions évoquées. Gardez aussi un oeil sur les options nécessaires pour avoir toutes les fonctions et l'équipement d'un éventuel deuxième vélo, sinon vous allez y laisser un bras. Taper "compteur vélo cardio altimètre cadence" dans un moteur de recherche pour voir ce qui existe chez Sigma, Polar ou Cateye par exemple. Pour le double de zeuros, un GPS donne tout ça, et en plus permet de se repérer plus facilement, comme celui-là par exemple : Le GPS qui me va bien

Pour démarrer, point n'est besoin d'outils sophistiquésr. Un compteur de base à 10€ qui donne la vitesse instantané et la distance, de chez D4 ou autre chose, et un petit tableau des développements et cadences sous les yeux fait fort bien l'affaire, si on est capable de savoir sur quel rapport plateau/pignon on est.

Si on veut avoir la cadence sous les yeux en permanence, et en moyenne, on pourra acquérir un compteur avec cadence (RPM), ou avec l'option cadence. Les GPS spécifiques au cyclisme le font bien, mais ils sont chers, et plus encore avec les capteurs optionnels : cadence, fréquence cardiaque, puissance. Les compteurs sophistiqués sans fil obligent à vérifier les piles. Les compteurs avec fil, pourtant fiables, robustes et peu coûteux ont disparu. Restent les compteurs sans fil, dont les chinois, où il bien difficile de discerner le bon grain du moins bon.